本文分析了有关斜抛和平抛的方程,附有对应的例题。
斜抛运动的参数方程
斜抛是抛体中比较常见的一类问题。最基本的斜抛运动可以通过分解来解决。
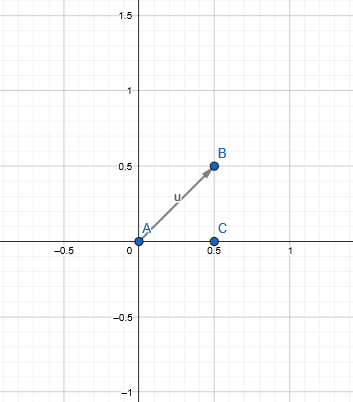
如图所示,A是质量为m的质点。现在,A具有一个斜向右上的初速度,设为\(v_0\),与\(x\)轴夹角设为\(\theta\)。引入一个参量\(t\),代表自抛出时刻开始经历的时间。
把\(x\)、\(y\)表述成关于\(t\)的量,得到如下参数方程。
\[\begin{cases} x=v_0\cos\theta\cdot t\\ y=v_0\sin\theta\cdot t-\frac12gt^2 \end{cases}\]这个方程是基本的方程。
轨迹方程
对参数方程,联立并消去参数\(t\),得到\(y,x\)间关系,即斜抛运动的轨迹,称为“轨迹方程”
把\(t\)用\(x\)表示,带入,得到\(y\)关于\(x\)的方程:
\[y=x\tan\theta-\frac{gx^2}{2(v_0\cos\theta)^2}\]这个式子被称作斜抛运动的轨迹方程。
轨迹方程是很有用的一个方程。注意到,这是一个开口向下的抛物线,而抛物线的性质在此也是十分有用的。来看几个轨迹方程的典型应用:
\(\sect1\) 如图,球1和球2从同一高度水平抛出,抛出点距离地面的高度为\(H\)。两球的初速度分别为\(v_1,v_2\)。球1抛出后刚好能够越过位于\(x_p\)处的竖直杆的顶端,并落在地面上的R点,R点距离O点的距离为R。球2抛出后落地与地面发生弹性碰撞,反弹后也刚好越过杆顶,并最终落在R点。求杆的位置和杆的高度。
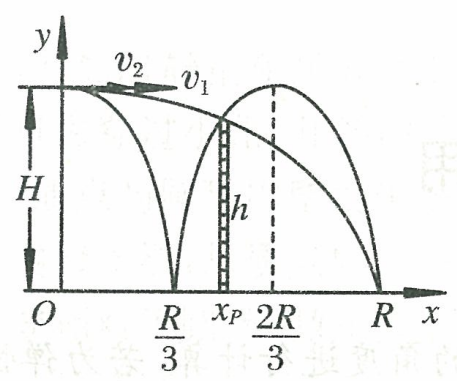
此题初见仿佛很复杂,但是实际上并不复杂。两个球都是平抛运动,还有交点这一要素,因此可以考虑使用轨迹方程。直接飞过杆的球1的轨迹方程是易于书写的:
\[y=-\frac{gx^2}{2v_1^2}+H\]但是对于球2,有人可能感到无从下手。没有关系,我们先写出它的轨迹方程,暂时不考虑反弹。
\[y=-\frac{gx^2}{2v_2^2}+H\]首先,求出球2的落点,这可以通过联立该轨迹方程和直线\(y=0\)来做到。
\[0=-\frac{gx^2}{2v_2^2}+H\]解这个关于x的方程,得到:
\[x_0=v_2\sqrt{\frac{2H}{g}}\]同理,我们可以得到球1的落点:
\[R=v_1\sqrt{\frac{2H}{g}}\]这时候,观察一下运动的特点。注意到,球2反弹后的抛物线和抛出时应当完全一致,这可以在y方向上分析其速度(x方向上速度一直是恒定不变的),根据弹性碰撞速度反向的特点来得到。也就是说,O和落地点之间的距离是二分之一的第一落点和第二落点之间的距离。那么,我们就知道了一个重要的式子:
\[R=3x_0\]接下来,注意到题目条件,两个球都是“恰好”飞过杆顶。于是我们可以联立球1的轨迹方程和球2反弹后的轨迹方程来得到杆的位置。
先求出反弹后的轨迹方程:
\[y=-\frac{g(x-2x_0)^2}{2v_2^2}+H\]即:
\[y=-\frac{g(x-\frac23R)^2}{2v_2^2}+H\]联立求解,过程中,还需要知道一个式子:
\[v_1=3v_2\]这个式子是很轻松就可以由\(R=3x_0\)导出的。
解方程,取合理解,得到:
\[x_p=\frac12R\]带入轨迹方程,就可以得到高度:
\[h=\frac34H\]这道题是直接使用的轨迹方程,在许多需要求轨迹交点的问题中是很好的方法。虽然在本题中使用显得较为繁琐,但是注意到这种方法思维难度很低,写出轨迹方程后按照数学方法解方程即可。
再来看一道体现另一种应用方法的题目:
\(\sect2\) 在高为h的平台上以初速度\(v_0\)抛射物块,请问抛射角为何值时,射程最远?
先写出轨迹方程:
\[y=x\tan\theta-\frac{gx^2}{2(v_0\cos\theta)^2}+h\]但是,题目要求的是x的最大值,而不是y的。这就比较麻烦,如果求反函数,计算量会比较惊人,有没有什么简单的办法呢?当然有。
在落点处,满足:
\[0=x\tan\theta-\frac{gx^2}{2(v_0\cos\theta)^2}+h\]把它进行一个三角函数变换:
\[y=x\tan\theta-\frac{gx^2}{2v_0^2}\cdot(1+\tan\theta)^2+h\]此时,这不仅是一个关于x的二次方程,还是一个关于\(\tan\theta\)的二次方程。那么,该方程应该有解:
\[\Delta=(2v_0^2x)^2-4(gx^2)(gx^2-2v_0^2h)\ge0\]解得:
\[x\le \frac{v_0\sqrt{v_0^2+2gh}}{g}\]此时:
\[\tan\theta=\frac{v_0}{\sqrt{v_0^2+2gh}}\]得到结果。
这种方法也是十分常见的。灵活运用二次函数的数学性质是解决该类问题的关键。
但是,我们要知道,把参数方程变形为轨迹方程实际上是丢失了“时间”这一信息的。也就是说,只有和时间无关的问题,才能使用轨迹方程。如果与时间有关,那么就必须特意考虑时间的信息。
\(\sect3\) 从左至右的水平地面上依次摆放三个质点a,b,c,三者共线。a与b相距\(l_1\),b与c相距\(l_2\)。现在同时将它们从初始位置抛出,已知质点b以初速度\(v_0\)上抛,质点c以某一初速度上抛。假设质点a的质量远大于质点b,且碰撞时间极短。要求质点a能碰到质点b和c,求出质点c的初速度和质点a的初速度满足的条件。
可以看到,这道题要求发生“碰撞”即两质点于同一时间到达同一位置,这显然就不是很适合使用轨迹方程了。
现在,我们先假设出质点a的抛射角度为\(\theta\)。直接考虑参数方程。要想和b发生碰撞,那么在同一时刻它们的x和y坐标应当分别相等。并且,碰撞必须在地面上发生,即y必须大于等于0
\[\begin{cases} x=l_1=v_a\cos\theta\cdot t_1 \\ y=v_0t_1-\frac12gt^2_1=v_a\sin\theta\cdot t-\frac12gt^2_1 \end{cases}\]因为质点b的质量远小于质点a的质量,所以这次碰撞不会对质点a的轨迹产生影响。分析质点a与质点c要能发生碰撞的条件。
\[\begin{cases} x=l_1+l_2=v_a\cos\theta\cdot t_2 \\ y=v_ct_2-\frac12gt^2_2=v_a\sin\theta\cdot t-\frac12gt^2_2 \end{cases}\]通过y的条件,联立可以解出质点c初速度满足的条件:
\[v_c=v_0\]通过数学方程,解出a的初速度满足的一个条件:
\[v_a\sin\theta=v_0\]另一个条件需要利用到碰撞发生在地面上这一物理事实,y大于等于0。
得到:
\[v_a\cos\theta=\frac{g}{2v_0}(l_1+l_2)\]这个题目就需要保留参数方程中关于t的条件,而不能盲目化成轨迹方程令其轨迹相交求解。
对于抛体运动轨迹方程的初级应用,灵活考虑题目条件,选取方法是最重要的。参数方程也不只有一种变形,还可以消去抛射角,或者进行某些特殊的操作来使解题更加顺利。不能死记硬背模板,灵活考量,仔细计算,才能最终做对题目。
文档信息
- 本文作者:DoubleCabbage
- 本文链接:https://doublecabbage.github.io/2022/07/22/projectile-motion/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)