本文分析了弹簧的串并联导致的总体劲度系数变化，并附有几道经典例题的解析。

弹簧的并联

并联的情况比较简单。考虑一些劲度系数各不相同（设为\(k_1,k_2,k_3,...\))但原长都一样的弹簧，将它们的两端各自接在两块木板上。

如图，这样就构成了一个并联的弹簧系统。如果我们固定左板，对右板施加一个水平向右的力\(F\)，并且假设这个力导致的弹簧伸长量为\(x\)。伸长量对各个弹簧应当一致。

假设整体的等效劲度系数为\(k'\)。此时，外力\(F\)应该与所有弹簧产生的合力大小相等方向相反。由胡克定律：

两侧同时除以\(x\)，得到并联弹簧的总等效劲度系数：

弹簧的串联

串联的情况就没有那么友善了。考虑一些劲度系数各不相同（设为\(k_1,k_2,k_3,..\))的弹簧，将它们首尾相连，固定好。这里假设弹簧都是轻质的，不受重力。

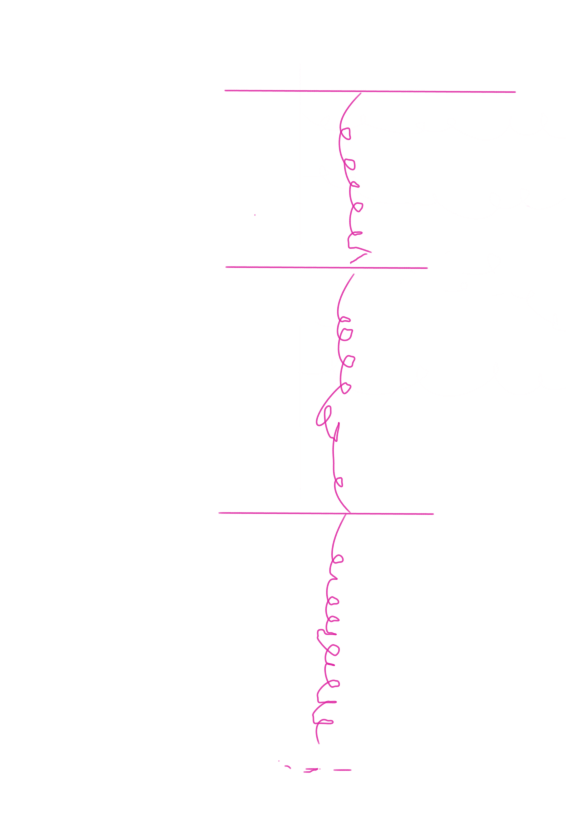
如图，这样就构成了一个串联的弹簧系统。固定最上方的板，对弹簧下端施加一个竖直向下的力\(F\)，假设由这个力导致的每个弹簧的伸长量为\(x_1,x_2,x_3...x_n\)。

假设串联的等效劲度系数为\(k'\)，总的伸长量是\(x\)。如果我们隔离任何一个弹簧进行分析，很容易就可以得到在此弹簧上面的一个弹簧对它的拉力与它对下面一个弹簧的拉力相等。即在弹簧之间的每个分界面上，拉力都是相等的。（注意，这个结论并不总成立，需要弹簧自己的质量为0，即轻质）。这个拉力是等于外力\(F\)的（对最下面的一个弹簧隔离分析得到这个结论）。

由胡克定律：

但是此时我们发现有些无从下手。按照胡克定律\(F=kx\)，要想求出\(k\)，就需要用\(F\)除以\(x\)，但这会导致分母上出现一个求和，无法下手。这时候我们希望什么呢？希望2式的求和出现在分子上，这样可以直接把它拆成若干个短分式相加的形式。

用2式除以1式：

感觉还是不好下手？把右侧的分式直接拆开！

注意到我们还有1式的条件，把分母上的\(k_1x_1\)替换成\(k_nx_n\)

约分，带回开始的式子。

这个结论的电阻的并联是一致的。

一些例题

\(\sect\) 1. 把一个弹簧测力计的弹簧剪去一小段。如果对这个新的测力计施加相同的力，它的示数和一个全新的没有剪弹簧的测力计的示数相比如何？

知道了上面的结论，我们做如下假设。假设剩下的弹簧劲度系数为\(k'\)，原有弹簧的劲度系数为\(k\)，剪去弹簧的劲度系数为\(k''\)。

根据串联规律，有：

得出：

得出：

然后，比较一下大小：

即\(k'>k\)。剪去弹簧的测力计的劲度系数变大了。那么，对于相同的力，指针移动的距离就应当减小，即示数应该比完好的测力计的示数要小。

\(\sect\)2.对于一个正方体，它的每个边上都是阻值为R的电阻。请问在它的立体对角线上的两端点之间（A、B两点之间）的等效阻值是多少？进一步地，如果每个边上都是劲度系数为k的弹簧，A、B两点间的等效劲度系数是多少？

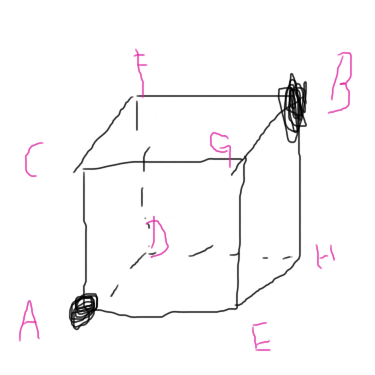
对于电阻的情况。C、D、E上的电势应该是相等的，因为整个系统是对称的。同样的，F、G、H的电势也是相等的。

于是，等效电阻就是AC、AD、AE并联，BG、BF、BH并联，中间6个并联之后再串联。等效电阻就很容易算出了。

那么对于弹簧也不难了。直接利用串并联公式，先算出3个和6个弹簧并联的劲度系数：

再串联：

如果对对称性的使用还抱有疑惑的话，也可以画出等效的复杂电路图（实际上并不复杂）并利用基尔霍夫方程组来求解。设出两点流入的电流，然后计算出各支路上电流，算出两点之间电势差，再除以流入的总电流即得等效电阻。然后就可以类似地处理弹簧的串并联关系了。